等加速度直線運動は実は簡単?3つの公式の意味と覚え方
高校物理で最初に習うのは運動ですね。
物理学の最も基本の部分なので最初に習うのは必然的なのですが、この分野で一番躓きやすいのが等加速度直線運動ですね。
物体の運動もそうですが、粒子の運動、分子の運動も等加速度運動が理解できていないと読み解いていくことが来ません。
コツをつかめばそこまで難しくないのですが、この等加速度運動で物理が嫌いになる人も多いと思います。
この分野を習ったときは、クラスの3割くらいが躓いて物理嫌いになってました。
本当は簡単なのに、躓いて物理嫌いにならないためにも、今日は等加速度直線運動をマスターし、物理学の最初の壁を乗り越えていこうと思います。
等加速度直線運動とは
皆さんはそもそも等加速度直線運動とはどのような運動か知っていますか。
加速度ってそもそもなんでしょうか。
まずは等加速度直線運動がどういう運動なのかを学んでいこうと思います。
加速度
加速度という言葉が突然出てきて戸惑う人もいるのではないでしょうか。
加速度とは単位時間当たりの速度の変化のことをいい、速度変化の度合いを表すので加速度といいます。
単位は主に$m/s^2$(メートル毎秒毎秒)を用います。
加速度が大きいほど速度変化が大きくなり、小さいほど速度変化は小さくなります。
小学校の算数の授業などではあまり気にしていなかったと思いますが、今までは速度が変化しない等速運動でした。
しかし皆さんも今まで生きてきて「速度が変化しない」なんてこと、そんなにないですよね。
車でも電車でも自転車で走っていても、だいたいは速度が変化します。
そこで高校ではその変化する速度がどういった割合で変化しているのか、ゆっくり速くなっていくのか、スポーツカーのようにスッと早くなるのか、それを考察するために加速度という概念が出てくるわけです。
等加速度直線運動
等加速度直線運動とは字のごとく一定の加速度で直線運動する運動のことです。
加速度が一定で普遍なので「等」という字を用いて等加速度、そして一直線上を運動するので直線運動。
合わせて等加速度直線運動になります。
ここで大事なのが加速度が一定なので、定数として考えることができることです。
実はこの加速度一定が大事になります。
3つの公式の意味と覚え方
さて等加速度直線運動が理解できたと思うので、いよいよ公式のほうへ移ろうと思います。
と、その前に加速度の式とこの分野でよく使うv-tグラフを最初に解説しておきます。
公式を覚えるよりもむしろこのv-tグラフが肝になってくるのでしっかり勉強していきましょう。
加速度の式
加速度は単位時間当たりの速度変化の度合いを表していました。
ここで変化量をΔ(デルタ)を用いて表すと加速度 a は下のように表せます。
$$a=\frac{Δv}{Δt}$$
ここで$v$は速度、$t$は時刻を表します。
この式を式変形すると
$$Δv=aΔt$$
となるので、ある時間で変化した速度はaΔtで計算できます。
先ほどお話ししましたが、等加速度直線運動ならば加速度は定数なので1次関数$y=ax$と同じ形をしていることが分かります。
(もし加速度が定数でないと1次関数の形にはならないので、定数が大事といったのはこのためです。)
v-tグラフ
さて加速度の式が$Δv=aΔt$であり、1次関数$y=ax$と同じ形なのでグラフで表現できそうですね。
($y$が$Δv$、$x$が$Δt$に相当し、グラフの傾きが加速度にあたります。)
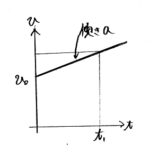
このように$y$軸が$v$、x軸が$t$のグラフをv-tグラフといいます。
このグラフは等加速度直線運動を覚える上で必須ですし、便利なので覚えておきましょう。
等加速度直線運動3つの公式
さていろいろ学んできましたが、いよいよ3つの公式の時間です。
とはいっても実はこの公式覚える必要すらありません。
なぜならv-tグラフと加速度の式を知っていればすぐに導出できるからです。
では1つずつ導出してみましょう。
①1つ目の公式 $v=v_0+at$
加速度の式は$Δv=aΔt$といいました。
しかしこれはあくまである時刻からある時刻までの速度変化の量を表すので、計算で求められた速度は実際の速度ではなく変化した速度の量(前時刻と後時刻の速度差)になります。
では初速度(ある時刻を基準としたときのその瞬間の速度のことです)を$v_0$としたとき、$Δt$秒後の速度$v$はどうなるでしょうか。
1次関数であることに着目すると初速度$v_0$は$y=ax+b$でいうところの切片bに相当することが分かります。
よって$y=ax+b$を等加速度で使えるように書き換えると、$v=at+v_0$となりそうです。
($y$を$v$、$x$を$t$、$b$を$v_0$、傾き$a$は加速度$a$に置き換えただけです。)
グラフからこの式がでてきましたけど、これって等加速度直線運動の1つ目の公式そのものですよね。
ただv-tグラフの1次関数の式を書いただけです。
つまり、v-tグラフが1次関数になることを知っていれば1つ目の式なんで覚える必要ないわけです。
学校にいる頭が賢い・物理が得意な人は必ずと言っていいほどまずv-tグラフを適当に書いて状況を整理します(もしくは頭の中で想像する)。
傾きと切片の位置に注意してあとは中学生の知識で解けてしまうわけですね。
さてこの調子で2つ目の公式に行ってみましょう。(これもグラフから導けます。)
②2つ目の公式 $x=v_0t+\frac{1}{2}at^2$
続いて2つ目の公式$x=v_0t+\frac{1}{2}at^2$を求めてみましょう。
実はこれもv-tグラフから求めることができます。
時刻$t_1$までの変位$x$は、下の4つの点で囲まれた台形の面積で求めることができます。
- 原点$(0,0)$
- $y$切片($t=0$のときの$y$の値、つまり$(0,v_0)$)
- $(t_1,0)$
- $(t_1,v_0+at_1)$
面積を求めるだけなので長方形($x_1$とします)と三角形($x_2$とします)にわけて計算してみましょう。
長方形は縦×横なので$x_1=v_0t$ですね。
三角形は底辺×高さ÷2なので(1つ目の公式$v=v_0+at$の式を使って式変形しています。)
$$x_2=\frac{t×(v-v_0)}{2}=\frac{t×(v_0+at-v_0)}{2}=\frac{t×at}{2}=\frac{1}{2}at^2$$
以上から、
$$x=x_1+x_2=v_0t+\frac{1}{2}at^2$$
2つ目の公式が導かれました。
面積求めるだけなので覚える必要ないですよね。
次は最後3つ目の公式です。
③3つ目の公式 $v^2-v_0^2=2ax$
最後3つ目の公式です。
3つ目の公式は上の1つ目と2つ目の式から導出できます。
簡単に言うとtを消すだけです。
とはいっても計算はちょっと複雑ですが、中学生でもできる計算です。
まずは1つ目の式を代入しやすいように$t=$の形にします。
$$t=\frac{v-v_0}{a}$$
これを2つ目の公式に代入します。
$$x=v_0×\frac{v-v_0}{a}+\frac{1}{2}a×(\frac{v-v_0}{a})^2$$
右辺第2項をちょっと計算
$$x=v_0×\frac{v-v_0}{a}+\frac{1}{2}a×\frac{(v-v_0)^2}{a^2}$$
さらに右辺第2項をちょっと計算
$$x=v_0×\frac{v-v_0}{a}+\frac{1}{2a}×(v-v_0)^2$$
両辺$×2a$
$$2ax=2v_0(v-v_0)+(v-v_0)^2$$
後は右辺を計算するだけです。
$$(右辺)=2v_0(v-v_0)+(v-v_0)^2=2vv_0-2v_0^2+v^2-2vv_0+v_0^2=v^2-v_0^2$$
これで3つ目の公式が出てきました。
まとめ
等加速度直線運動の公式の意味は理解できましたか。
- 1つ目の式はただのv-tグラフの1次関数の式を書いただけ
- 2つ目の式はv-tグラフの面積を計算しただけ
- 3つ目の式は1つ目と2つ目から$t$を消去しただけ
こう見ると大事なのはv-tグラフとv-tグラフが持つ便利な性質であって、式はどうでもいいことがわかります。
また2つ目の式よく見ると実はただの2次関数の式なんです。
そう考えると、等加速度直線運動なんて本当に数学の延長で意外とできそうな気がしませんか。
この分野を学んだときは躓きかけましたが、この公式の覚え方というよりも導出の仕方を理解したことで、等加速度運動の理解も深まり得意分野に変わりました。
なにせ、1次関数と2次関数とそこから$t$を消しただけの式で問題が解けるんですから、むしろラッキーなくらいです。
ちなみに本来物理学は微分・積分方程式ですべてを表します。
今回の3つの公式は微分・積分を知っていれば加速度の定義式 $a=\frac{dv(t)}{dt}$ からすぐに導けます。
(といっても3つ目の公式の導出は同じ方法になります。)
今回学んだ3つの式は今後複雑な運動を読み解くうえでも非常に重要な式なので、しっかり理解していきましょう。

ディスカッション
コメント一覧
まだ、コメントがありません